What are suffix trees?

Suffix trees are a tree representation of a string and all its suffixes. Consider the string mississippi$ . It is convenient to make sure the strning ends in a symbol not found elsewhere. The suffixes of mississippi$ are:

• mississippi$
• ississippi$
• ssissippi$
• issippi$
• ssippi$
• sippi$
• ippi$
• ppi$
• pi$
• i$
• $

In tree form, this becomes:

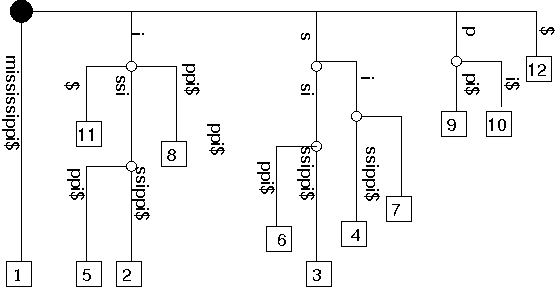
Once given this suffix tree , it is easy to search for a string: one just goes down the tree following the string.

Most good suffix tree construction algorithms also require a suffix link at each node. A suffix link can be understood by taking into account the string leading to a node. For every node, consider this incoming string (not just the edge, but the whole string from the root) and take the first character to obtain a slightly shorter string. Now follow it from the root and you will end up at the node corresponding to that node's suffix link. If this was confusing, maybe an illustration helps (suffix links as dashed arrows):

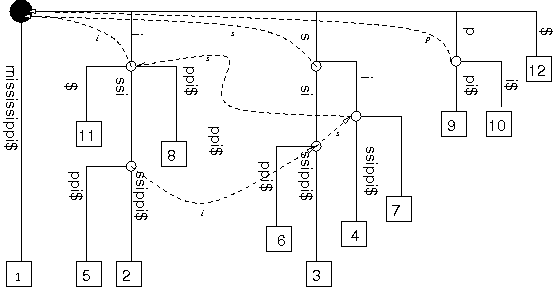
It is not absolutely clear what the root's suffix link should point to. A traditional solution is having it point to itself.

Representation of a suffix tree

The number of characters in the branches of a suffix tree grows with $N^2$, where $N$ is the number of characters in the string. However, there is a way to represent suffix trees in $O(N)$ space. This is based on keeping the original string and representing branches by indices into this string. For example, the branch from the root to the leaf marked as mississippi$ above could be simply saved as the pair $(1,12)$ marking the beginning and the end of the string. Thus, each branch needs only a pair of integers.

There are several ways one could implement a tree. The most widely used one is to make it a collection of nodes. Each node then has the following fields:

Start and End

: The start and the end points of the incoming branch.

Children

: Pointer to the first child or null if it is a leaf.

Brother

: Pointer to the next sibling or null.FatherPointer to the node's father.

Suffix Link

: A node's suffix link.

Note that a father link is not strictly necessary . This means that it possible to have (and even build) a tree without father links .

Kurtz has done many interesting analysis of suffix trees and, in particular proposed a representation where the incoming edge is represented as a pair of integers with a different meaning:

Start

: A position in the original string where the string to the node (the full string from the root) appears. Note that there may be several positions in the string which fulfil this criterion. For representation purposes it does not matter which one is taken.

String Depth

: How deep is the node, measured by the number of characters that must be followed from the root to reach it. Note that this is different from node depth which is the number of intermediate nodes that are passed en route to the node.

In this representation, the edge reaching a node is labeled by the string which goes from $Start+father.String_Depth$ to $Start+father.String_Depth$.

This seems awkward compared to the more direct Begin/End pair outlined above. However, for the price of a small inconvenience when accessing an edge label, many other operations become easier (the full benefits are hard to explain, but become apparent to one actually writing code to work with these structures).

Implementation

Here you can find my implementation of suffix trees in C++. I have implemented both McCreight's and Weiner's algorithms. Ukkonnen's algorithm can be shown to be just a variation of McCreight's (see Kurtz's paper, link below), so you can consider that that one is implemented as well.

This code is used as the basis of my dotted tree software, but independent of it.

It does not support strings with the NUL character ('0' in C/C++). As usual, this is used as the terminal character for the string, like the dollar sign in the above examples.

Bibliography

1. Stefan Kurtz. Reducing the Space Requirement of Suffix Trees. Software--Practice and Experience, 29(13), pages 1149-1171, 1999.
2. E.M. McCreight. A space-economical suffix tree construction algorithm. Journal of the ACM, 23:262-272, 1976.